表1 自衡和積分對象的特性描述對比
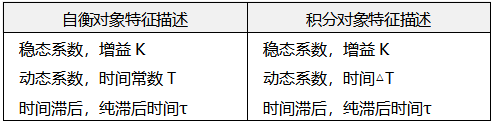
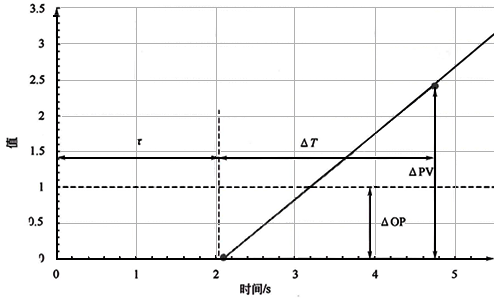
圖1 積分對象響應曲線
如圖1的積分對象響應曲線所示,對積分對象我們使用響應曲線中過程變量按一定斜率穩(wěn)定變化后的任一點來確定△PV,從PID控制器輸出階躍變化的起點到該點的時間為τ+△T的總時間。從△PV處沿斜線反向做直線與開始位置的坐標橫軸相交,PID控制器輸出階躍變化的起點到該交點為純滯后時間τ,交點到△PV的時間為△T。
積分對象的增益和自衡對象的增益計算公式一樣:
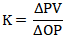
積分對象和自衡對象的特性可以用基本一樣的參數進行描述。下面的試驗證明:積分對象的Lambda整定方法也可以直接借鑒自衡對象的公式。
為了方便分析,我們定義基準積分對象的模型參數為:穩(wěn)態(tài)系數,增益K=1;動態(tài)系數,時間△T=1s;時間滯后,純滯后時間τ=1s
第一步首先只考慮純比例控制不考慮積分作用,計算公式與自衡對象的Lambda整定方法類似:
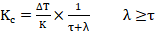
對基準積分對象使用λ=0/τ/3τ=0/1s/3s的設定值階躍響應曲線,如圖2所示。從響應曲線可以看到:λ=τ時過程變量設定值階躍響應曲線有超調無振蕩,是最優(yōu)閉環(huán)響應;如果使用更小的λ,設定值階躍響應曲線就會振蕩,比例作用太強,積分對象也會像自衡對象一樣振蕩;如果λ=3τ,設定值階躍響應就會比較緩慢。λ的正確選擇應該是基于純滯后時間。推薦λ≥τ,這個取值范圍也和自衡對象的Lambda整定方法類似。
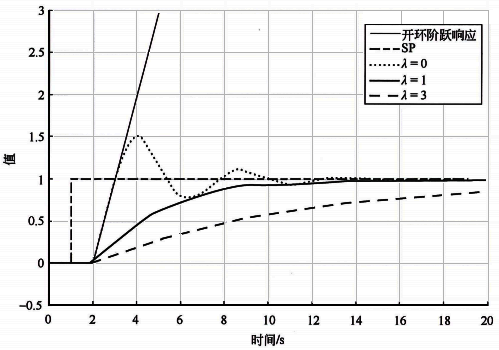
圖2 基準積分對象不同λ的設定值階躍響應
看起來純比例控制器控制積分對象的效果非常好,積分對象的積分環(huán)節(jié)可以代替PID控制器的積分作用,實現閉環(huán)設定值階躍響應無穩(wěn)態(tài)余差。但是實際工業(yè)應用中,使用純比例控制器控制積分對象仍存在余差。因為在實際被控對象中干擾的來源多種多樣,干擾可能來自被控對象的輸出,也可能來自被控對象的輸入,這兩類干擾引起的余差是不同的。
對圖3所示閉環(huán)控制系統進行設定值和擾動階躍變化,其響應曲線如圖4所示。設定值階躍和輸出階躍擾動d?時純比例控制器可以實現無余差,但是輸入階躍擾動d?時純比例控制器有余差。這就是實際使用中,積分對象雖然已經有積分作用,但是使用純比例控制器還是有余差的原因。
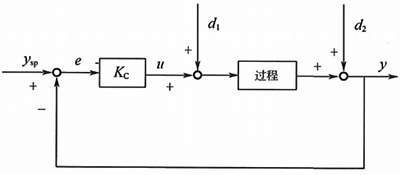
圖3 純比例控制框圖
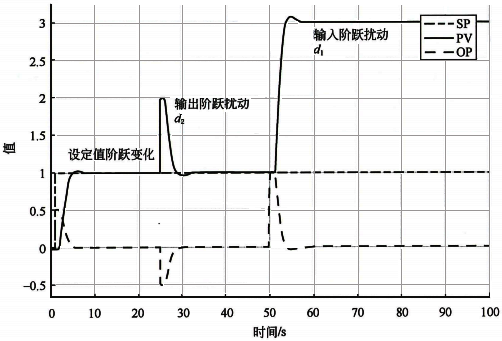
圖4 積分對象純比例控制的設定值、輸出擾動、輸入擾動的階躍響應
即使被控對象是積分對象,考慮到擾動的復雜性,為了消除各種擾動可能導致的余差,也推薦使用比例積分控制而不是純比例控制。
關鍵是積分時間如何設置才能既避免振蕩又能消除余差。積分時間太大,閉環(huán)響應不會振蕩,但是消除余差的能力會比較弱;反過來積分時間太小,則閉環(huán)系統超調加大甚至會振蕩。
針對基準積分對象,選擇λ=τ,則:
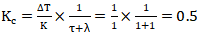
不同積分時間的設定值階躍響應如圖5所示。可以看出:純比例不振蕩,積分作用太強了引起振蕩,積分作用弱了消除余差比較慢,增強積分作用閉環(huán)響應超調更嚴重,更容易振蕩。增加積分作用后過程變量的超調量明顯增加,這是由積分對象的積分作用和比例積分控制器的積分作用的雙重作用造成的。最佳的積分時間能最快速消除余差而且還不會引起振蕩。
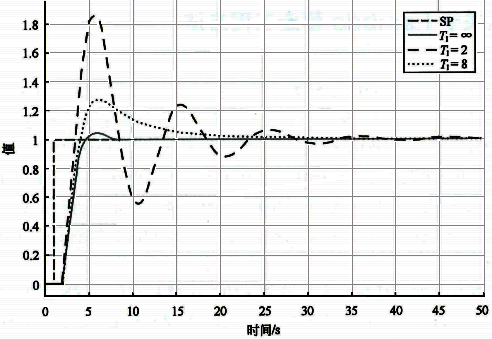
圖5 基準積分對象比例積分控制器不同積分時間的設定值階躍響應
△T會隨著在響應曲線上的選點不同而變化,所以△T并不是積分對象的本質特性,不能用于確定積分時間。根據分析知道:對積分對象而言,當使用比例積分控制時,積分時間足夠大,比例增益和積分時間的乘積滿足式(4-16)時,積分對象不會振蕩,這個結論的理論推導見附錄。但是積分對象的閉環(huán)響應會出現超調,而且基本上一直都有超調。
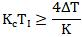
推薦的不振蕩最小積分時間為:
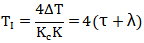
對積分被控對象,使用比例積分控制器的Lambda整定公式:
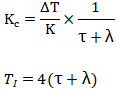
積分對象的Lambda整定方法可以歸納為:微分不用、積分足夠、比例適當。







